异构材料中“非均匀变形诱导强化”5个基本问题的讨论
编审:刘畅
近几年来,材料研究的报道中,出现了一个"异质结构材料(Heterostructured Materials)"的概念。这一话题已成为材料科学与工程领域各种研讨会的焦点议题之一,最近发表的研究论文也比较多。在应力载荷作用下,这类材料表现出“非均匀变形诱导强化”(heterogeneous deformation induced strengthening, HDI 强化)效应[1],有时翻译成"异质变形诱导强化"。
1.“异质变形诱导强化”如何量化?
HDI强化,从历史的沿革来看,其源头应该是始于上世纪60至70年代,来自于Ashby[2,3]以及Brown和Stobbs提出的背应力和几何必需位错(GND)概念和机制。当时所讨论的题目是:deformation in plastically non-homogeneous materials (非均匀塑性变形材料)和 hardening of dispersion-hardened crystals(弥散强化晶体的硬化),也就是heterogeneous deformation induced hardening (非均匀变形强化)。目前文献中对于HDI强化效果的量化,主要是通过测量样品中(样品整体水平)的背应力(back stress)来完成。背应力的产生,是因为不均匀塑性变形区域交界或强化障碍边界处,为了兼容塑性变形在该处的失配会累积几何必需位错(GND),这些GND带来定向长程内应力, 使得后续位错运动所需应力提高,从而造成材料强度提高。背应力的定量测量与所需实验步骤,见问题3.
2. 异质结构是否总是能够带来额外的强化效果?
答案是“异构不一定带来额外强化”。例如,许多异质结构材料,在性能上会低于基于各组成区域的性能按照“混合法则(rule of mixtures, ROM)”推估的平均值(以等应力和等应变两种状态作为极端情况),或者,性能可以通过ROM充分描述(意味着异质区域间界面的贡献很小)。此时并没有令人信服的证据显示“异构设计”会带来引人注目的性能与机制。沿用复合材料常用的ROM经验规则已经足够。这种情况下,比如当A、B性能反差不够大、A/B界面不够多(密)时,给材料另外再贴上一个异构标签并不必要。
事实上,对于A/B组合,当A和B为宏观尺寸(如在毫米量级)时,人们通常不会太多强调这一A/B复合为异构材料。而当A/B在尺度上减小至微纳米量级的交互堆叠时,材料的宏观性能自然会显著受其异质结构特性影响(这将引出下面的问题3),演化成典型的异构材料。换言之,仅仅依靠单一界面是远远不够的。实现材料的"异构化",必需将硬质与软质两个部分各自变成微小单元并充分混合(见Q#3),即“先细化,再混均”。
换言之,我们问题的关键是异质结构在什么情况下能够带来额外的强化效应。答案是材料只有在经过特殊异构设计时(另见Q#5),额外强化效果才会出现,即将硬质区(A)与软质区(B)在空间适当调控分布,达到很小的特征尺度(λ)时才会发生。这个特征尺度λ可以是渐变(A-B)结构(或与之对应的硬度)的周期(如正弦波形),也可以是硬软区具有锐利A/B界面时的A-B中心距。据此可定义结构(或其对应的硬度)梯度,其单位例如GPa/mm(见Q#3中图2)。要想额外强化效应高,需要设计显著的结构梯度,即很小的λ,意味着单位体积/长度内存在大量A-B对和A/B(弥散或锐利)界面(如图1中间示意图所示),同时选择硬度反差大的A与B。这样会产生更多、更密集的协调塑性失配的需求,在各界面区域引发额外的几何必需位错(GND)密度,从而增加背应力与强化效应(在Q#3中称为II型背应力)。我们将其定义为"结构梯度硬化"(SGH),以区别于教科书中的传统强化机制。需要强调的是,SGH特指通过有意识设计硬软区分布、引入的高梯度结构所产生的超额强化,这部分效应无法依据“混合法则”(ROM)简单地预测,是超越ROM的存在。
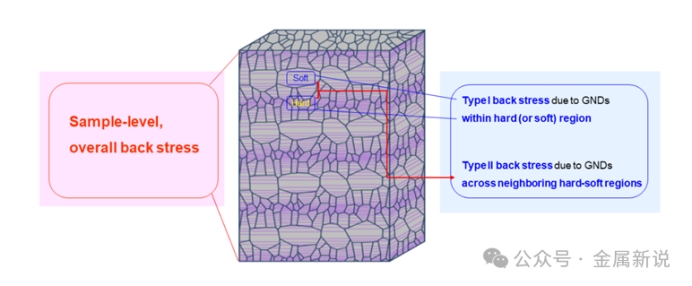
Figure 1 Adapted from Ref. 4, Z. Cheng, L. Bu, Y. Zhang, H. Wu, T. Zhu, H. Gao, L. Lu, Unraveling the origin of extra strengthening in gradient nanotwinned metals, Proceedings of the National Academy of Sciences of the USA 119 (2022) e2116808119.
3.如何定量结构梯度强化(SGH)及其相关背应力?
在实验上,样品整体的背应力可通过往复“加载-卸载-再加载(LUR)”测试中的滞后回环进行测量。然而,这种整体背应力(图1左)并不能直接完全归因于来自人为设计的异质结构。因为总体背应力是可能源自多种因素的集成效应与普遍现象。因此,需将其分解为I型与II型分量。如图1右所示,I型分量存在于异构材料内各均质硬(软)区中,源于区内晶粒间塑性非均匀变形(即使晶粒尺寸均匀)导致的GND背应力;即使是在均匀尺寸的超细晶(特别是纳米晶)金属中,由于晶界密度大,I型背应力可在数百兆帕量级。II型分量,则量化硬/软区之间结构梯度(对应硬度梯度、应变梯度)产生的额外强化,才是我们关注的结构梯度强化。唯有II型背应力才能真实地反映由异质结构设计所带来的SGH这一“净附加值”。
下面提供一个具体的数据分析案例,来帮助理解如何得到II型背应力并评价其重要性。
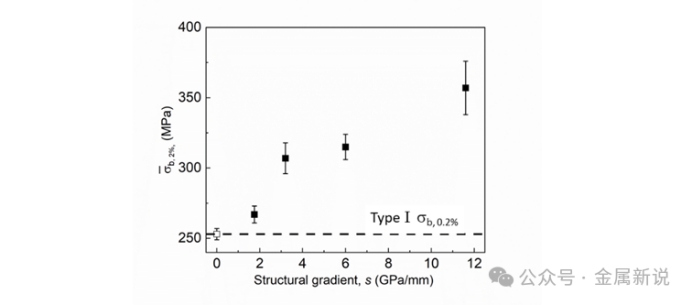
Figure 2 Adapted from Ref. 4, Z. Cheng, L. Bu, Y. Zhang, H. Wu, T. Zhu, H. Gao, L. Lu, Unraveling the origin of extra strengthening in gradient nanotwinned metals, Proceedings of the National Academy of Sciences of the USA 119 (2022) e2116808119.
图2所示的数据是通过以下步骤获得的:
i) 测量总背应力(纵坐标, 数据点):通过LUR测试中的滞后回环测得;
ii) 评估I型背应力(虚线):对仅含硬质(或软质)成分、组织的均质样品单独测试背应力,再根据硬/软区体积分数加权平均(ROM混合法则);
iii) 分离出II型背应力:总背应力减去I型分量即得II型背应力,即SGH分量。
图2中4个不同样品的硬/软区体积分数相同,故这4个HS材料由ROM算得的I型背应力是一样的。但它们内部硬/软各片区的厚度不同,导致4个样品中的结构梯度(反映为单位长度内的硬度变化,GPa/mm)不同。图2的实验显示:II型背应力随结构梯度增大而显著增加:这一结果凸显了仅报告总背应力(如近期文献中的常规做法)的局限性。
从这个例子也可以看出,II型背应力才是“异构”的关键一环:它是在软、硬区总体积分数定了以后,将软、硬异质在空间构造成不一样的区域与组合,来改变、提升性能的一项, 而I型背应力则是“异构”的出发点(起跑线)。
图2中例子的具体定量分析如下:四个样品在2%应变下的总背应力σb,0.2%值介于265至360 MPa之间,虚线所示的I型分量是由混合法则(ROM)计算得出的I型背应力(253 MPa),代表的是结构梯度为零这一极限情况时的背应力值。总背应力与I型分量的差值(范围12-107 MPa)即为II型背应力,随样品制备中人为引入结构梯度的增加而增大。图2中结构梯度最大的样品(如图中强度梯度为12 GPa/mm的样品),II型背应力占总背应力的30%(107/360),该样品显然可被视为典型的异构材料;反之,当结构梯度较小时(如图中强度梯度2 GPa/mm的样品),II型背应力仅为12 MPa,此时该HS材料实际上并不那么“异构”—其强度主要源于A(硬区)中细小的孪晶/晶粒尺寸,而异质结构设计(A/B/A/B堆叠)带来的“附加值”小于总强度的5%(12/265)。
4. 通过构建方程来计算异构材料强度时需注意什么?
需要特别注意避免重复计算问题。比如,在建立异构材料强度方程时,许多最近发表的文章简单地将细晶强化与背应力硬化直接相加。其实,测得的背应力中,I型背应力占比很大,源自晶界处累积的几何必需位错(GND)。而晶粒尺寸细化效应,同样可归因于位错在晶界的塞积,已通过经典晶界强化公式(如Hall-Petch关系)充分描述。换言之,二者反映相同的物理本质:均是塞积的位错。所以,晶界强化项与背应力项不可叠加,否则会导致机理层面的重复计算。
II型背应力需单独剥离出来,以量化和凸显“异构”的贡献—结构梯度等设计参数导致的额外强化(SGH)。
5. 能否再突出一下异构材料的核心机制与设计主张?
i) 异构的核心:在于A-B区空间组合排列的协同效应,具体是将界面密度与空间分布特性,通过结构梯度参数(对应强度梯度)予以量化。该结构梯度导致II型背应力。我们通过测得的II型背应力来定量表征并评估非均质造成的结构梯度带来的额外强化。在工程实践中,异构材料可通过调控内部结构梯度,实现力学性能的调控与优化(包括在保持相同成分组成及软硬区总体比例的条件下)。
所有异质结构材料都会有背应力,包括I型和II型背应力,比如双相或多相合金(如钢、钛合金和超合金)、功能梯度材料、沉淀硬化合金、具有双峰或多模晶粒尺寸的多晶体、多层膜或片层微观结构,等等。其中许多异构材料中,结构梯度与II型背应力不够大。多晶合金、多晶单质金属内部也会有背应力,因为塑性变形本质上具有非均匀性。例如,在特定加载下,不同晶粒的施密特因子差异可以很大,造成位错在晶界塞积(GND)。如前面提到的,在纳米晶金属中测得的背应力甚至可在数百兆帕量级。但这时只有I型背应力,II型背应力为零。从微观结构角度来看,晶粒大小分布较窄的多晶单质金属通常不被视为异构材料。
ii) 异构材料设计步骤:
设计异质结构材料的第一步,是选择“原材料”:即硬(A)区与软(B)区本身所用的材料(包括影响其软硬程度的晶粒尺寸等),和硬、软区二者的总体积分数(比如60%-40%)。这些,决定了基线(I型)背应力的大小。选好原材料当然是异构的基础,但性能可从已知机制和公式(如ROM)预估,且一旦选定,不再随第二步的不同设计而变化。
第二步,是真正挑战智力的“异构”设计(heterostructuring),即操控A、B区(各自)的大小、数目、形状、非均匀空间分布,特别是结构梯度(或对应的强度梯度参数),产生并最大化额外(II型)背应力,以提升与优化力学性能。
更为详细的讨论与分析,将在我们日后发表于《Scripta Materialia》的Viewpoint文章中阐述,敬请关注。
预印本已放在arXive上,网址为:
http://arxiv.org/abs/2509.01908
参考文献:
[1] Y. Zhu, X. Wu, Heterostructured materials, Progress in Materials Science 131 (2023) 101019.
[2] M.F. Ashby, Work hardening of dispersion-hardened crystals, Philosophical Magazine 14 (1966) 1157-1178.
[3] M.F. Ashby, Deformation of plastically non-homogeneous materials Philosophical Magazine 21 (1970) 399-424.
[4] Z. Cheng, L. Bu, Y. Zhang, H. Wu, T. Zhu, H. Gao, L. Lu, Unraveling the origin of extra strengthening in gradient nanotwinned metals, Proceedings of the National Academy of Sciences of the USA 119 (2022) e2116808119.
